Understanding GANs
Generative Adversarial Networks (GANs) are one of the exciting model architectures that gave rise to the increasing popularity of machine learning in the space recently. GANs are generative models, meaning that they create new data that resembles the training data, for example, by creating realistic images of human faces. The images below were created by GANs:

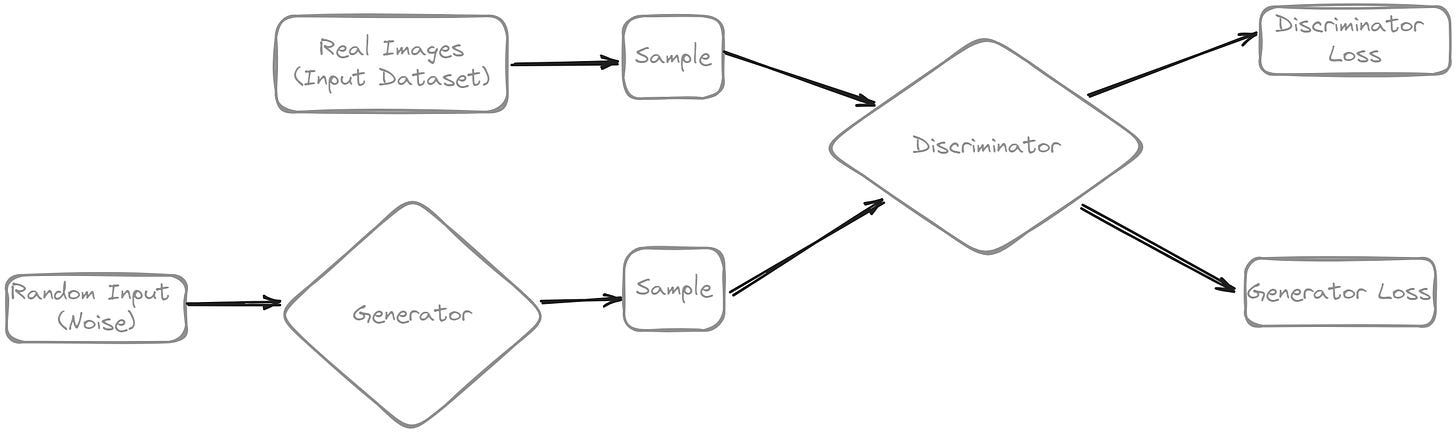
quite realistic, right? In a GAN, there are two fundamental blocks (neural networks), the generator and the discriminator.
Generator: The generator takes in random input as noise and generates data samples that are similar (in the latent space) to the input data.
Discriminator: The discriminator is just a binary classifier that outputs whether the sample image is real or fake. The input used by the discriminator comes from both the generator and the input dataset.
Generative and Discriminative models
A generative model focuses on the latent distribution of a dataset and returns an example, basically generating what is most likely to be a part of a dataset, while a discriminative model makes predictions on unseen data based on conditional probability and can be used for classification and regression tasks.
The goal of a generator model is to produce samples that are indistinguishable from the real data, while that of the discriminator is to correctly distinguish between the real and the generated samples.
The Training Process
The discriminator is trained like a deep network classifier; for example, if the input is real, it will return a standardized output of 1, and if the input is fake, it will return an output of 0. This process allows the discriminator to understand the features that contribute to real images.
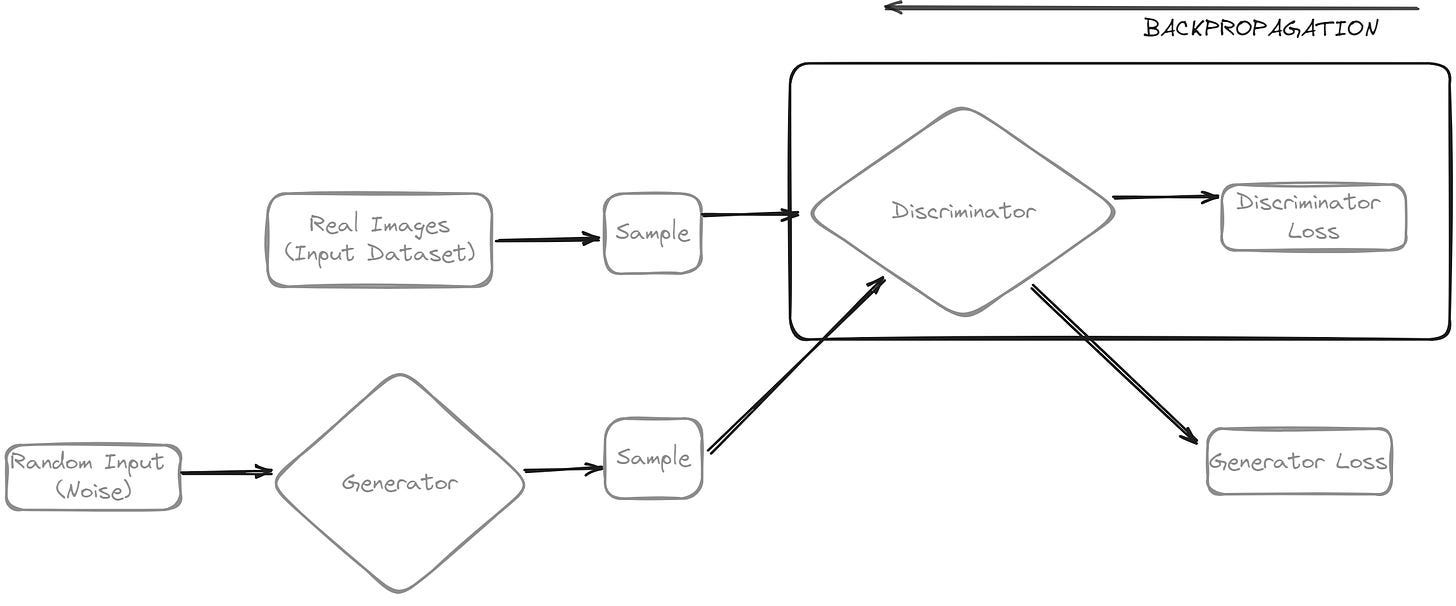
In the figure above, the two sample boxes represent the data sources feeding into the discriminator. During the discriminator training, the generator does not train (i.e., its weights are frozen) while it generates data for the discriminator to train on. The discriminator connects to two loss functions; the generator loss is neglected during the discriminator training, and only the discriminator loss is used. When the discriminator classifies the input data from the data source samples, the discriminator loss penalizes it for any misclassification it makes, and then its weights are updated through backpropagation from the discriminator loss through the discriminator network.
Simultaneously, the generator generates images that should return a standardized output of 1 (this is so that it can match the real images), so we then train the generator by backpropagating the target values all the way back to the generator, i.e., training the generator to generate images that the discriminator will think are real.
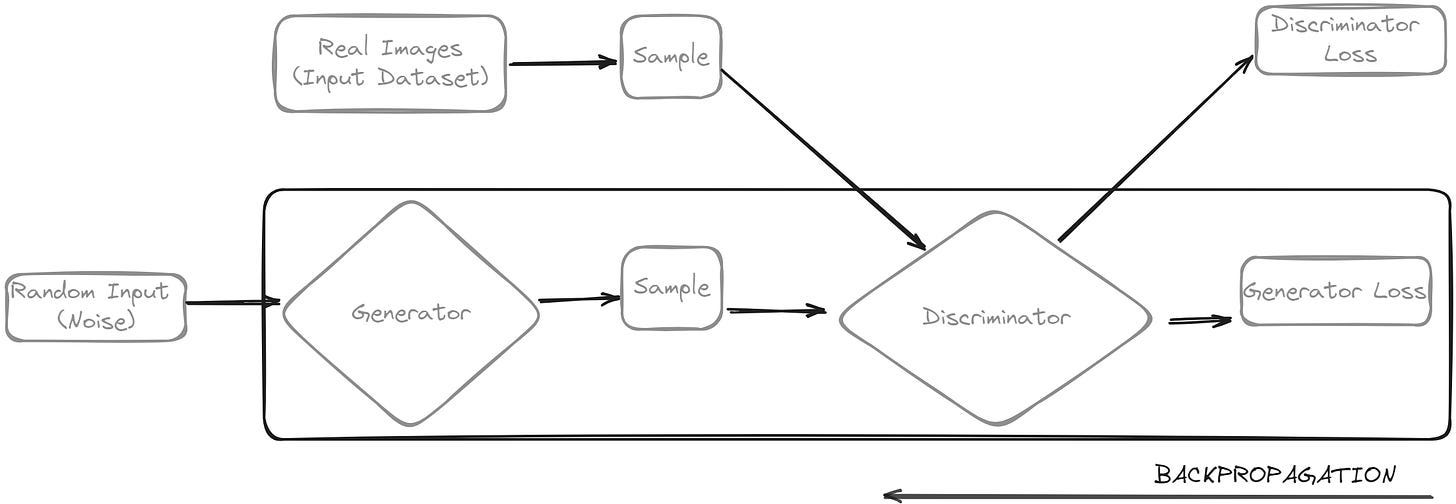
Neural networks require some form of input; in its most basic form, a GAN takes noise as input (uniform distribution). The generator then transforms the noise into a meaningful output. By introducing noise, we get the GAN to produce a wide variety of data (within its latent space), sampling from different places in its target distribution. In training a simple neural network, we know that we alter weights and add biases to reduce the error (loss) of its output, but in our case, the generator is not directly connected to its loss; rather, it feeds into the discriminator network, which then produces the output we are trying to affect. The generator loss penalizes the generator for producing a sample that the discriminator network classifies as fake (remember, the goal here is for the generator to produce images as good as the sample of the real images).
Using backpropagation to adjust the weights in the right direction by calculating the weights impact on the output (i.e., how the output would change if you changed the weight). In our scenario, the final output is affected by the weight impact of both the discriminator and the generator, so the backprop starts at the output and flows through the discriminator and the generator.
At the same time, we do not want the weights of the discriminator to change as we train the generator. Trying to hit a moving target makes the problem a lot harder (no convergence). So, when we use backprop to obtain the gradient, we will then use the gradients to only change the generator weights.
The training goes on in alternating steps, i.e., the generator is constant while the discriminator trains for one or more epoch, and the discriminator is constant while the generator trains for one or more epoch, which puts the models into a competition to improve themselves. Eventually, the generator creates images that the discriminator cannot tell the difference between, and the discriminator is not that good at identifying the tiny difference between real and generated. The GAN converges to produce real and authentic images because the more the generator model improves, the more the discriminator model also improves.
Example
Imagine you have a GAN trained to generate realistic images of handwritten digits, such as digits 0–9. The generator would take random noise as input and generate images that look like handwritten digits. The discriminator would then evaluate whether a given image is a real handwritten digit or a generated one.
During training, the generator gets better at creating more realistic digits, while the discriminator improves its ability to distinguish between real and generated digits. This process continues until the generator generates images that are so realistic that the discriminator can no longer reliably differentiate between real and generated samples.
Convergence
As the generator improves with training, the discriminator gets “worse” in the sense that it can’t tell the difference between real and fake, so successful generator training will get the discriminator to 50% accuracy. This poses a problem for GAN convergence because the discriminator’s feedback gets useless over time. If the GAN continues to train past that time, the generator will eventually start to train on useless feedback.
Loss
In GANs, the loss function is a crucial component that guides the training process by quantifying the performance of both the generator and discriminator. The primary objective of GANs is to find a Nash equilibrium where the generator produces realistic data, and the discriminator is unable to differentiate between real and generated samples.
Generator loss: The generator’s loss function evaluates how well the generator is performing in generating realistic samples.
One common choice for generator loss is binary cross-entropy. The generator aims to maximize the probability that the discriminator classifies its generated samples as real.
Discriminator loss: The generator’s loss function evaluates how well the generator is performing in generating realistic samples.
One common choice for generator loss is binary cross-entropy. The generator aims to maximize the probability that the discriminator classifies its generated samples as real.
Thanks for reading this article, if you are interested in more things like this, you can subscribe to my substack here.